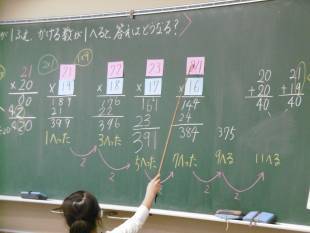２位数×２位数のかけ算の筆算を学習。かけ算の筆算をする必要性を生み出すために　＜かけられる数が１ふえ、かける数が１へると、答えはどうなるだろう？＞　という課題で学習を進めた。
　まず、２０×２０＝４００を計算。「これからかけられる数を２１にするとどうなる？」と問うた。「２０ふえるよ」といきなりの発言。「え？２０ふえるってどういうこと？」ここで、かけ算の話になり、２０の２０こ分が、２０の21こ分と考えると２０の１こ分が増えるんだと説明が始まった。さらに、実際に筆算をして２０×２０と２１×２０の一段目、二段目を比べさせた。納得。
　「かけられる数が１ふえると答えが増えるってことは、かける数を１９にすると、答えはもどにもどるね（２１×１９）」と問うた。問いやこだわりを持たせるためにしかけたわけである。「うん、もどるもどる」「え、もどらない」「わからない」３つの意見となったので、実際に筆算をすることにした。「あれ、答えが１減っている」「たし算はもどるのに」「やっぱりね」と様々なつぶやきがあった。何か減っていきそうだと感じたらしく、次はどうなるか試し始めた（２２×１８）「次は、３減っている」次は、その次は・・・。「こだわり」が表れてきた。「１，３，５，７と答えが減っていく」「減る数が２ずつ増えている」「たぶんそれは、２０×２０だから２ずつ増えたんだ」
　「それなら、３０×３０だったら３ずつか？」
「やってみたい」とどんどん筆算を試し始めた。「え？同じだ」「は～ん」筆算を進めるうちにまたつぶやきが出てきた。「きまりがわかった」とも。数字の同じ部分をさがし、１，３，５，７と減っていく根拠を見つけていた。「～さんがいったことはどんなことか」ペアで話し合わせたり、他者説明させたりして、話し合いを洗練させていった。そうすることで、筆算を見直すきっかけともなった。
　４０×４０にしたらどうだろう？５０×５０は？６０×６０は？と今日学んだことをもっと試してみたくなった様子だった。
　次の日、なんでそうなるかまで図で示して、この学習を終えた。筆算が使える道具になっていっただろうか。
　明日の研究発表会での授業でも筆算がより使える道具となってほしいと願いながら、子供を見取っていきたい。