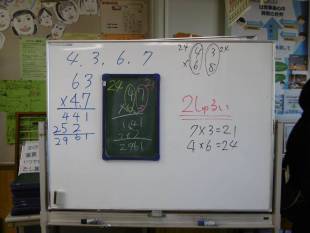２位数×２位数の筆算を利用して、条件にあう計算を考えることを本時のねらいとした。「自分で試行錯誤して筆算づくりに没頭する楽しさ」や「どう考えてつくったか話し合い、きまりを整理することで、数のおもしろさに出合う楽しさ」を子供が味わうために次の３つの手立てをとった。

手立て１：条件をそろえたり、身につけた計算の仕方の技能を活用できる問題を設定したりすることで、試行錯誤しながら数理的な処理に没頭できるようにする。
１，２，４，８を使って、４８＋２１の筆算を提示した。たし算の計算は以前やったこともあったので、答えが同じになる４つの計算をすぐ見つけることができた。

これを受けて、かけ算ではどうか？と投げかけた。分科会では、いったん「ひき算はどうだろう？」となげかけてから「かけ算は？」と流れたほうがよりスムーズであったとご意見をいただいた。子どもの意識の流れをもう少し整理してもよかったとふり返った。

　たし算で見つけた方法で試したけれど、実は見つけられないのがこの問題のおもしろいところで、交換法則だけはたし算と同じだが、その後がなかなか見つけられずにいた。答えの一の位に着目した子は、なんとかそれを手がかりにたし算の筆算とは違う組み合わせを考え始めた。「同じになった」大きくつぶやく。見つけたことをだれかに知ってもらいたくて仕方ない様子がちらほら見られた。　できたものを小黒板に出させた。３枚中1枚だけうらにして提示した。すぐに答えを見せず、少し類推させたかったからだ。自分で試行錯誤して見つけられなかったとしても黒板に出てきたことから、違った角度から筆算を見て、ちょっとのひらめきが出てくるかもしれない。そうしたら、また試したくなる「こだわり」が出てくることも期待した。

手立て２：「数をいれかえるということはいつでも言えることか」「今友達が言っていることはどういうことか」という観点をもって、ペアや全体で話し合う場を設定することで、自分が見つけたきまりと友達の見つけたきまりから、計算をもう一度とらえなおすことができるようにする。
　見つけ方を順番に説明。交換法則はかけ算でも成立すること、答えの一の位は必ず同じになるようにそこを一番に考えたということが出てきた。

　４種類ずつ見つかった同じ答えの筆算。２つの例で、「いつでもいえるのか」という観点をもたせるため、もう1例出してみた。４７×６３である。実はこれは２種類しか同じ答えが見つからない。さっきまでと何が違うか探り出す子どもたち。ここでは、計算に没頭する姿が見られた。
　十の位、一の位をそれぞれたてに見てきまりを見つけ出した。それぞれたての九九の答えが同じときは４種類、違うときは2種類なのだ。1人目が説明した。3分の２はわかっていない様子。2人目が説明した。「は～ん」というつぶやき。でもまだわかっていない子多数。3人目が説明した。「えっ」というつぶやき。ほとんどの子がわかってきたなと見取ったので、ペアで説明させた。ここでわかっていない子もこの話し合いで理解できると見取った瞬間だったからである。きまりを整理することで、なぜそうなるかわからなくてもなんだかおもしろいなと感じていたことが、つぶやきから見取れた。

手立て３：見つけたきまりに合わせて、自分で試す場を設定することで、条件をみたすときまりがあり、さらに数のイメージを広げることができるようにする。
　2種類見つかる場合と4種類見つかる場合があることを知り、4種類見つかる場合の筆算をいくつか自分で試す時間である。説明で時間がかかったため、最後に１つだけ出してもらったが、もう少し時間をつくって数のイメージを広げたかった。そのために、３例目ではもう筆算をつくらせるのではなく、筆算を出して確かめるだけにすれば時間が短縮できたと分科会で教えていただいた。
　筆算づくりということを考える子を育む教材としてこれからも研究していきたい。