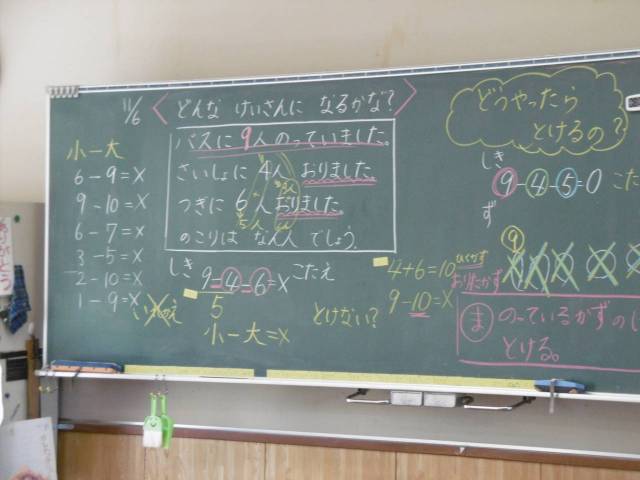バスに9人のっていました。さいしょに4人おりました。つぎに　　人おりました。のこりはなん人でしょう。

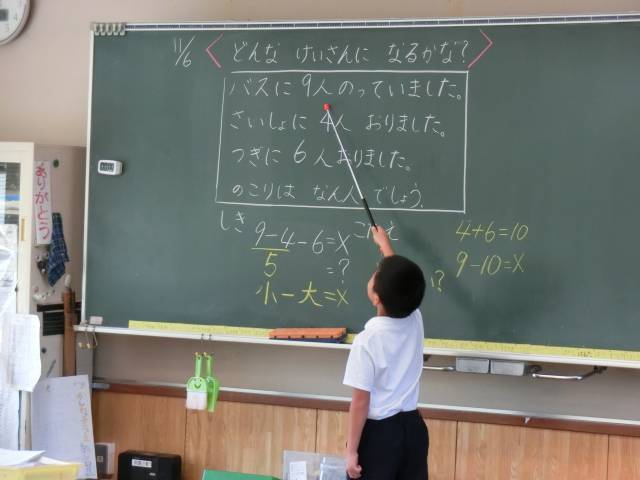
　つぎにのあとに数字が入っていないから、９－４－？＝？になるという。「では、ここに数字をいれたら、解けるんだね？」と問い返すと1人だけから「解けないかも」というつぶやきも聞こえてきたが、残りのみんなは「うん」とうなずいたので、数字をいれた。
　「6」という数字をいれたので、式は９－４－６となった。式をつくりながら「え？」「うん？」という声。「９－４－６＝×です」「９－４－６＝？です」という発言が出てきた。みんなそれぞれのかきかたで、式をノートに書いていた。「なぜ×なの？」「なぜ解けないの？」問い返すと、２つの意見が出てきた。
　1つ目は、９－４＝５で、５－６はできないから。
　2つ目は、４＋６＝１０で、９－１０はできないから。
どちらも、小さい数から大きい数はひけないというのです。
そのへんをみんなで説明しあった。

　たとえばを出しながら、説明しあったあと、「どうやったら解けるの？」と問い返した。「降りた4人を3にかえるといいよ。」「次に降りた5人を4人にかえてもできるよ。」という発言が続いた。本当にそうなのか、図をかいてもらった。図と式の数を合わせて確認した。「本当に答えが0人になるね。」みんなで確認しあった。

　「なぜ解けない？」「どうやったら解けるの？」と教師が問い返したり、子供が「たとえば」や「もし」を使って説明ができたりしたことで、それぞれ自分なりに解ける問題ってどんなものかを考えられるようになっていった。
　そこで、プリントを配り、自分で解ける問題を作り、式・図・答えまでかいてみることにした。

　自分なりに、問題を見直し、解けるように問題を決める姿がそれぞれのペースで見られた。どんどん思いつく子は、次々とプリントを取ってかいていた。ゆっくり考える子は、確認しながらすすめていた。

　自分で解ける問題をつくり解いていくことで、与えられただけの問題を解くのではなく、自分で問題を理解して、つくる楽しさやこだわりがあった。今回は、「ずをつかってかんがえよう」の導入として、バスの乗り降りの問題設定による決める姿だったが、もっと生活に密着した、たとえば、買い物にいってお金が足りなくなると困る状況のような教材に変化させていき、もっと未来を志向する子を目指していきたいと振り返った。